Advancements in Format Abstraction for Sparse Tensor Algebra Compilers: Techniques and Challenges

The world of data is evolving faster than ever. With the rise of machine learning, artificial intelligence, and big data analytics, sparse tensor algebra has emerged as a crucial player in this landscape. However, efficiently processing these sparse tensors poses significant challenges for developers and researchers alike. That’s where Format Abstraction for Sparse Tensor Algebra Compilers come into play—they optimize computations involving high-dimensional arrays with mostly zero entries.

Yet, there’s another layer to consider: format abstraction. This concept can transform how we design our compilers by enabling them to handle various data formats seamlessly. Imagine a tool that adapts dynamically to different storage schemes while optimizing performance at every turn! Format abstraction for sparse tensor algebra compilers promises not only efficiency but also flexibility in dealing with complex datasets.

Join us on this exploration of why format abstraction is essential in compiler design and what innovations are shaping its future. As we delve deeper into the intricacies of sparse tensor algebra compilations, you’ll discover how this approach can revolutionize computational tasks across numerous fields—ultimately pushing boundaries you may have thought were fixed.

What Are Sparse Tensor Algebra Compilers?

Sparse tensor algebra compilers are specialized tools designed to optimize computations involving sparse tensors—mathematical structures that represent high-dimensional arrays with a significant number of zero entries. These compilers enhance performance by transforming tensor operations into efficient code, tailored for various hardware architectures.

Unlike traditional compilers focused on dense data structures, sparse tensor algebra compilers leverage the inherent sparsity in data. This allows them to skip over zero values during calculations, reducing both memory usage and computational overhead.

The key lies in their ability to intelligently manage different storage formats suited for sparse data. By analyzing the specific characteristics of input tensors, these compilers can choose the most effective algorithms and strategies for execution. As a result, they enable faster processing times and improved resource allocation across diverse applications—from machine learning models to scientific simulations.

The Need for Format Abstraction in Compiler Design

As datasets grow larger and more complex, the demand for efficient computation intensifies. This is particularly true in sparse tensor algebra, where traditional methods struggle to keep pace.

Format abstraction emerges as a vital solution. It allows compilers to handle diverse data formats seamlessly. By abstracting these formats, developers can focus on optimizing algorithms without getting bogged down by specific representations.

This approach enhances flexibility. Different applications may require different storage schemes based on their unique requirements. Format abstraction enables dynamic selection of the most suitable format at runtime.

Moreover, it fosters innovation within compiler design itself. New techniques and improvements can be implemented easily without overhauling existing infrastructures. The adaptability offered through format abstraction is essential in navigating the complexities of modern computational needs.

Challenges with Sparse Tensor Algebra

Sparse tensor algebra presents unique challenges that demand innovative solutions. One significant issue is the representation of data. Sparse tensors often contain a large amount of zero values, leading to inefficiencies in storage and computation.

Another challenge lies in the complexity of operations. Traditional linear algebra techniques may not directly apply, requiring specialized algorithms tailored for sparse structures. This adds layers of intricacy to compiler design.

Moreover, performance optimization becomes critical yet complicated. Developers must balance memory usage with computational speed while maintaining accuracy across various tensor formats. The right approach can significantly impact both execution time and resource consumption.

Integrating compatibility across different hardware and software environments poses additional hurdles. Each platform might handle sparse data differently, complicating the compilation process further. Addressing these issues is essential for advancing the field and enhancing overall efficiency.

Exploring Format Abstraction for Sparse Tensor Algebra Compilers

Exploring format abstraction for sparse tensor algebra compilers opens new avenues in computational efficiency. By decoupling data representation from algorithm implementation, this approach allows for greater flexibility in handling diverse tensor formats.

Different algorithms can leverage the most suitable storage methods without being tied to a specific representation. This adaptability is crucial as it enables compilers to optimize performance dynamically based on the input data characteristics.

Moreover, format abstraction facilitates easier integration of emerging storage techniques into existing frameworks. As researchers develop innovative formats, compiler designers can incorporate these advancements seamlessly.

This exploration encourages collaboration among various fields such as machine learning and scientific computing. The synergy created by shared insights fosters rapid growth and innovation within the domain of sparse tensor algebra compilers, pushing boundaries further than ever before.

Innovations in Format Abstraction for Sparse Tensor Algebra Compilers

Recent advancements in format abstraction for sparse tensor algebra compilers are reshaping the way we handle data. By developing new algorithms, researchers can optimize storage and access patterns effectively.

One notable innovation is the introduction of adaptive formats. These dynamically adjust based on input characteristics, allowing for better memory utilization and improved computational efficiency. This adaptability plays a crucial role in handling various workloads seamlessly.

Moreover, machine learning techniques are increasingly being integrated into compiler design processes. They enable predictive modeling for format selection, ultimately enhancing performance across different architectures.

Another exciting trend involves hybrid formats that combine the strengths of existing representations. These hybrids can balance flexibility and speed while minimizing overhead costs.

As these innovations unfold, they promise to simplify complex operations within sparse tensor computations, paving the way for more efficient applications in diverse fields such as artificial intelligence and big data analytics.

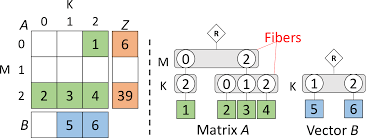
Types of Formats: Block, Compressed, and Hybrid

When it comes to sparse tensor representations, several formats stand out: block, compressed, and hybrid. Each format has unique characteristics that cater to different computational needs.

Block format groups non-zero elements into dense blocks. This method enhances memory access patterns during computation. It’s particularly effective for operations where data locality is critical.

Compressed formats reduce the storage footprint by eliminating zero entries entirely. Formats like COO (Coordinate List) or CSR (Compressed Sparse Row) store only non-zero values alongside their indices. This efficiency makes them suitable for large-scale applications.

Hybrid formats combine the strengths of both block and compressed methods. They adapt based on the sparsity structure of the tensor, offering flexibility while maintaining performance levels across various computations.

These types of formats help optimize resource use in sparse tensor algebra compilers, driving innovation in fields such as machine learning and scientific computing.

Advantages and Challenges of Using Format Abstraction

Format abstraction offers significant advantages for sparse tensor algebra compilers. It provides flexibility in handling various data formats, allowing compilers to optimize performance based on the specific needs of a computation. This adaptability can lead to increased efficiency and faster execution times.

However, challenges exist alongside these benefits. Implementing format abstraction requires complex algorithms that may introduce overhead during compilation. Additionally, developers must ensure that abstractions do not compromise the precision of calculations or increase memory usage unnecessarily.

Adopting multiple formats also complicates compiler design. Balancing between different approaches while maintaining simplicity can be daunting. As advancements continue in this area, understanding both advantages and challenges will be crucial for future developments in sparse tensor algebra compilers.

Implementing Format Abstraction in a Compiler

Implementing format abstraction in a compiler involves creating layers that can flexibly handle various sparse tensor formats. This flexibility is essential for optimizing performance across different hardware architectures.

One approach is to define an intermediate representation (IR) that captures the essential properties of each format. This IR serves as a bridge between high-level tensor operations and low-level implementations, allowing for targeted optimizations.

Compiler designers must also incorporate algorithms capable of dynamically selecting the best format based on specific use cases and data characteristics. Utilizing machine learning techniques can further enhance this adaptability by predicting optimal formats during runtime.

Robust testing frameworks are vital here too, ensuring that the compiler behaves predictably with various input tensors. By focusing on modular design principles, developers can create compilers that easily adapt to new advancements in sparse tensor algebra without requiring extensive rewrites.

Real-Life Applications of Sparse Tensor Algebra Compilers

Sparse tensor algebra compilers find their footing in various real-world applications, showcasing their versatility. One prominent area is machine learning, where they enable efficient operations on high-dimensional data. This capability accelerates tasks such as image recognition and natural language processing.

In scientific computing, these compilers play a crucial role. They optimize simulations that involve large datasets, making complex calculations manageable and faster. Researchers can tackle problems in physics or biology with greater precision thanks to improved computational efficiency.

Telecommunications also benefits significantly from sparse tensor algebra compilers. They enhance signal processing tasks by managing the vast amounts of data generated during transmissions.

Additionally, recommendation systems leverage these compilers to analyze user interactions with items effectively. By handling sparse matrices efficiently, businesses can deliver more personalized experiences to their customers while optimizing resource use.

Future Developments in Format Abstraction for Sparse Tensor Algebra Compilers

The landscape of sparse tensor algebra compilers is rapidly evolving. Emerging techniques are pushing the boundaries of format abstraction, making these tools more efficient and versatile.

Researchers are exploring adaptive formats that can dynamically adjust based on input data characteristics. This could lead to significant performance improvements across various applications.

Another exciting trend involves integrating machine learning into compiler design. By leveraging AI-driven optimization strategies, future compilers may automatically select the best format for a given computation.

Cross-platform compatibility is also in focus. Developers aim to create abstractions that work seamlessly across different hardware architectures, enhancing portability and usability.

Moreover, collaboration between academia and industry is expected to accelerate innovation in this field. Joint efforts will likely yield novel approaches that enhance both speed and accuracy in sparse tensor operations.

Conclusion

The exploration of format abstraction for sparse tensor algebra compilers reveals a landscape rich with potential and innovation. As computational demands grow, the ability to efficiently manage sparse data structures becomes increasingly important. Format abstraction serves as a crucial bridge, enabling compilers to optimize performance across diverse hardware configurations while managing various storage formats.

With ongoing advancements in technology, the challenges faced by sparse tensor algebra will likely evolve. Innovations in compiler design are essential for addressing these issues and ensuring that we harness the full power of machine learning and scientific computing applications.

As industries continue to embrace data-driven solutions, investing time into enhancing format abstraction methodologies could pave the way for significant breakthroughs in both academic research and practical implementations. The journey towards refined sparse tensor algebra compilers is only just beginning, but it holds promise for exciting developments ahead.